About

Rankpoll is an easy way to create ranked polls for you and your community. There are many problems with traditional first-past-the-post voting. Rankpoll allows you to use a system that helps solve these problems, by allowing voters to rank their favorite options instead of just choosing one favorite.

See how it works by looking at an example.

To make the system more transparent, you can see how votes were counted to arrive at the final result. However, if you don't care about the details you can simply create your poll, share it with your voters and rest assured that the result is fair and accurate.

Why should I care about voting systems?

Everybody experiences voting in their life in some form or another: elections, internet polls, team decisions at work, trying to decide what to eat in a group of friends. If you ever participate in a voting system, you probably also care that your one voice is heard. Understanding the voting system being used is the only way to know that you and everyone else is being fairly represented.

Not caring about the voting system being used is like playing a board game where your host just made up the rules, but everyone for some reason agrees that the game is probably fair, since the rules were so easy to make up. Just because something is simple and the first thing you think of, doesn't mean it's fair and good at what you intended it for.

What's wrong with just voting normally?

Most people intuitively use a system called first-past-the-post voting, where each person gets to vote for 1 option and the option with most votes wins. This is also called plurality voting. This system has multiple problems, as shown in this video by CGP Grey.

Ranked voting

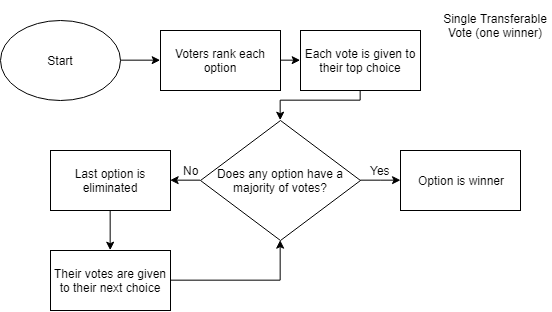
These problems can be mitigated using a system called Single Transferable Vote (STV). It works by letting voters rank their favorite options. After counting the first choices, if no one has more than half of the votes, you can eliminate the least popular option, and run the poll again as if that option wasn't available. Eventually, one option will have the majority of votes and can be declared the winner.

Droop Quota

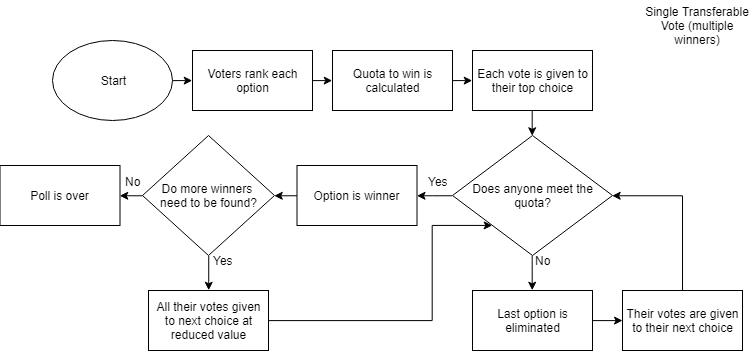
When multiple options are allowed to win, a trick can be deployed to make sure each winning option has met some minimum amount of votes, instead of being handed the win for having the most remaining votes. If 1000 people vote and 4 options need to be selected, instead of requiring 250 votes, we can require only 201 votes. Since, if 5 options had to reach that quota, there would need at least 1005 votes. This is called the "Droop Quota", and can be calculated like so:

Gregory Surplus Allocation

When multiple options are allowed to win, sometimes the first option to reach the quota will have more votes than the quota. If nothing is done with these votes, it actually punishes voters for backing popular options, as their votes are wasted, similar to how voters backing unpopular options in plurality voting waste their votes.

What we want to do is distribute them in some way to their next choice, to reward backers of popular options and allow them to get more representation in the final result. When doing an STV election with physical papers, multiple approaches can be used usually involving sampling a random subset of ballots and redistributing those.

When doing the election digitally, however, we can easily use the most fair system called Gregory Surplus Allocation. This allows all backers of a popular option to be represented but at a reduced value. If an option has 100 backers and only needs 90, it has 10 surplus votes. All 100 votes are given to their next choice but now they're only worth 0.1 votes. For all practical purposes, it's still 10 votes that have been distributed.

Weighted First Preference

To make it more likely that STV will produce a good result, a tie-breaking algorithm is neccessary. When eliminating the option with fewest votes, sometimes there may be multiple options tied for last place. Instead of eliminating all of them, it may be preferred to break the tie. Here, we can use an algorithm called Weighted First Preference, as described in "Random tie-breaking in STV" by Jonathan Lundell.

When multiple options are tied for elimination, we tally up how many voters preferred each one over all the others (weighted by their ballot's current weight). The option with the highest tally is marked as safe. This continues until only one option remains, which is then eliminated.

In the case that the remaining options tied for elimination are also tied in preference, a random one is chosen, instead of eliminating both or leaving the poll without a conclusion.

As Lundell points out, using each ballot's ranking of options to break ties breaks with the principle "later-no-harm", meaning that the rankings beyond your first choice shouldn't be able to affect the outcome unless your first choice is eliminated. However, this particular method of tie breaking preserves a method Lundell calls "later-no-direct-harm", meaning your rankings of your second and third choices, will never directly help them in a tie-break against your first choice.

Even though "later-no-harm" is technically violated, it may still be satisfactory to prevent tactical voting in that, as pointed out by Hill and Gazeley (Voting Matters issue 15, 2002 p.15):

"[Voters] would not be so tempted [to vote tactically] if they felt confident that later preferences were as likely to help earlier ones as to harm them, and if they could not predict the effect one way or the other. At present, we see no reason to doubt that these requirements are met."

See how tie-breaks work by looking at an example.

Approval Voting

If STV doesn't work for your specific case, approval voting may be preferred.

Approval voting is very straight forward: each voter can vote on as many options as they'd like, and the option that has been chosen the most times wins.